动态规划（dynamic programming）

动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。基本思想是将问题的求解过程化为多步选择或决策的结果，在每一步决策上，列出各种可能的选择，舍去那些肯定不能成为最化解的局部解。最后一步得到的解必是最优解。其适合解决具有以下两个特性的问题。

动态规划的特性 求解每个子问题仅仅一次，并将其结果保存在一个表中，以后用到时直接存取，不重复计算，节省计算时间。自底向上计算。
1. 最优子结构：问题的整体最优解中包含着它的子问题的最优解。
2. 子问题重叠性：第i+1步问题的求解中包含第i步子问题的最优解，形成递推公式
算法设计步骤
1. 分析优化解的结构
2. 递归地定义最优解的代价
3. 自底向上地计算优化解的代价保存并获取构造最优解的信息
4. 根据构造最优解的信息构造优化解

Longest Increasing Subsequence

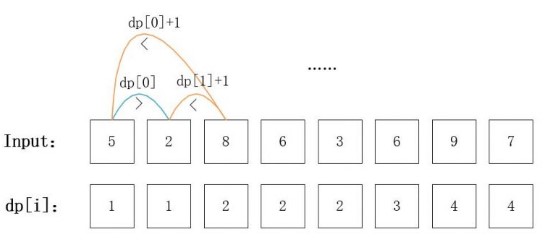
iven an unsorted array of integers, find the length of longest increasing subsequence. For example, Given [10, 9, 2, 5, 3, 7, 101, 18], The longest increasing subsequence is [2, 3, 7, 101], therefore the length is 4. Note that there may be more than one LIS combination, it is only necessary for you to return the length. Your algorithm should run in O(n²) complexity. Follow up: Could you improve it to O(n log n) time complexity?

方法一

递推公式：

$\\dp[i]=max \left \{ dp[j] | 0 < j < i; a_j < a_i\right \}+1$

 private static int LIS(int[] input){
     if(input.length<=0) return 0;
     int len=input.length;
     int result=0;
     int[] dp=new int[len];
     for(int i=0;i<len;i++){
         dp[i]=1;
         for(int j=0;j<i;j++){
             if(input[j]<=input[i]&&dp[j]+1>dp[i]) dp[i]=dp[j]+1;
         }
         result=Math.max(result, dp[i]);
     }
     return result;
 }

算法复杂度：

$\\O(n^2)$

空间复杂度：

$\\O(n)$

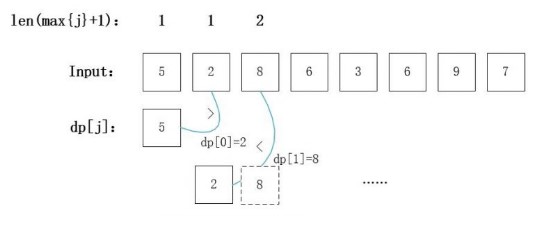
方法二 建立dp[i]数组，dp[i]表示最长不降子序列的长度为i时，该序列的最小最末元素为dp[i]。因为dp[i]本身是一个有序的数组，顾可以采用折半查找。

递推公式：

$\\dp[i]=min \left \{ a_j | a_j > dp[i-1] \right \}$

class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        int len = 0;
        for (int num : nums) {
            int index = Arrays.binarySearch(dp, 0, len, num);
            if (index < 0) {
                index = -(index + 1);
            }
            dp[index] = num;
            if (index == len) {
                len++;
            }
        }
        return len;
    }
}

算法复杂度：

$\\O(nlog^2)$

空间复杂度：

$\\O(n)$

Climbing Stairs

You are climbing a stair case. It takes n steps to reach to the top. Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

public class Solution {
    public int climbStairs(int n) {
        if (n == 1) {
            return 1;
        }
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

public class Solution {
    public int climbStairs(int n) {
        double sqrt5=Math.sqrt(5);
        double fibn=Math.pow((1+sqrt5)/2,n+1)-Math.pow((1-sqrt5)/2,n+1);
        return (int)(fibn/sqrt5);
    }
}

House Robber

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night. Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.

递推公式：

$\\dp[i]=max ( dp[i-1] , dp[i-2] + nums[i] )$

class Solution {
    public static int rob(int[] nums) {
        if(nums.length==0) return 0;
        if(nums.length==1) return nums[0];
        int[] dp = new int[nums.length];
        for(int i = 0; i<nums.length; i++) {
            if (i < 2) {
                dp[i] = i - 1 >= 0 ? Math.max(nums[i], nums[i - 1]) : nums[i];
            } else {
                dp[i] = Math.max(nums[i] + dp[i - 2], dp[i - 1]);
            }
        }
        return dp[nums.length-1];
    }

    public static void main(String[] args){
        int[] nums = {5,2,6,3,1,7};
        System.out.println(rob(nums));
    }
}

Maximum Subarray

Find the contiguous subarray within an array (containing at least one number) which has the largest sum. For example, given the array [-2,1,-3,4,-1,2,1,-5,4], the contiguous subarray [4,-1,2,1] has the largest sum = 6.

递推公式：

$\\dp[i] = max \left \{ dp[i-1]+nums[i], nums[i]\right \}$

class Solution {
    public int maxSubArray(int[] nums) {
          if(nums.length==1)return nums[0];
        int result=nums[0];
        int re=nums[0];
        for (int i = 1; i < nums.length; i++) {
            result=Math.max(result+nums[i], nums[i]);
            if(result>re){
                re=result;
            }
        }
        return re;
    }
}

Coin Change

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1. Example 1: coins = [1, 2, 5], amount = 11 return 3 (11 = 5 + 5 + 1) Example 2: coins = [2], amount = 3 return -1. Note: You may assume that you have an infinite number of each kind of coin.

递推公式：

$\\dp[i] = min\left \{ dp[i-1],dp[i-2],dp[i-5],dp[i-7],dp[i-10] \right \} + 1$

class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount+1];
        for(int i=0;i<=amount;i++){
            dp[i]=-1;
        }
        dp[0]=0;
        for(int i=0;i<=amount;i++){
            for(int j=0;j<coins.length;j++){
                if(i-coins[j]>=0&&dp[i-coins[j]]!=-1){
                    if(dp[i]==-1||dp[i]>dp[i-coins[j]]+1)
                        dp[i]=dp[i-coins[j]]+1;
                }
            }
        }
        return dp[amount];
    }
}

Triangle

Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below. For example, given the following triangle

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).

递推公式：

$\\dp[i][j] = min \left \{ dp[i-1][j-1],dp[i-1][j] \right \} + nums[i][j]$

 public static int triangle(List<List<Integer>> triangle){
     if(triangle == null || triangle.size() <= 0) return 0;
     List<List<Integer>> dp = new ArrayList<>();
     for(int i=0;i<triangle.size();i++){
         List<Integer> subDp = new ArrayList<>();
         for(int j = 0;j<triangle.get(i).size();j++){
             if(i == 0){
                 subDp.add(triangle.get(0).get(0));
             }
             else{
                 if(j-1 < 0){
                     subDp.add(dp.get(i-1).get(j)+triangle.get(i).get(j));
                 }
                 else if(j>=triangle.get(i-1).size()){
                     subDp.add(dp.get(i-1).get(j-1)+triangle.get(i).get(j));
                 }else{
                     subDp.add(Math.min(dp.get(i-1).get(j-1),dp.get(i-1).get(j))+triangle.get(i).get(j));
                 }
             }
         }
         dp.add(subDp);
     }
     int min = Integer.MAX_VALUE;
     List<Integer> list = dp.get(dp.size()-1);
     for(int i=0; i<list.size(); i++){
         min = list.get(i) < min ? list.get(i) : min;
     }
     return min;
 }

Minimum Path Sum

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path. Note: You can only move either down or right at any point in time. Example 1:

[[1,3,1],
 [1,5,1],
 [4,2,1]]

Given the above grid map, return 7. Because the path 1→3→1→1→1 minimizes the sum.

递推公式：

$\\dp[i][j] = min \left \{ dp[i-1][j],dp[i][j-1]\right \} + grid[i][j]$

class Solution {
    public int minPathSum(int[][] grid) {
        if(grid==null||grid.length==0) return 0;
        int row=grid.length;
        int col=grid[0].length;
        int[][] dp = new int[row][col];
        dp[0][0] = grid[0][0];
        
        for(int i=1;i<row;i++){
            dp[i][0]=dp[i-1][0]+grid[i][0];
        }
        for(int i=1;i<col;i++){
            dp[0][i]=dp[0][i-1]+grid[0][i];
        }
        for(int i=1;i<row;i++){
            for(int j=1;j<col;j++){
                dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+grid[i][j];
            }
        }
        return dp[row-1][col-1];
    }
}

Dungeon Game

The demons had captured the princess (P) and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of M x N rooms laid out in a 2D grid. Our valiant knight (K) was initially positioned in the top-left room and must fight his way through the dungeon to rescue the princess. The knight has an initial health point represented by a positive integer. If at any point his health point drops to 0 or below, he dies immediately. Some of the rooms are guarded by demons, so the knight loses health (negative integers) upon entering these rooms; other rooms are either empty (0’s) or contain magic orbs that increase the knight’s health (positive integers). In order to reach the princess as quickly as possible, the knight decides to move only rightward or downward in each step. Write a function to determine the knight’s minimum initial health so that he is able to rescue the princess. For example, given the dungeon below, the initial health of the knight must be at least 7 if he follows the optimal path RIGHT-> RIGHT -> DOWN -> DOWN. | -2 (K) | -3 | 3 | | -5 | -10 | 1 | | 10 | 30 | -5 (P) | Notes:

The knight’s health has no upper bound.

Any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.

class Solution {
    public int calculateMinimumHP(int[][] dungeon) {
        if(dungeon.length==0) return 0;
        int dp[][] = new int[dungeon.length][dungeon[0].length];
        int row = dungeon.length;
        int col = dungeon[0].length;
        dp[row-1][col-1] = Math.max(1,1-dungeon[row-1][col-1]);
        for(int i=col-2;i>=0;i--){
            dp[row-1][i]=Math.max(1,dp[row-1][i+1]-dungeon[row-1][i]);
        }
        for(int i=row-2;i>=0;i--){
            dp[i][col-1] = Math.max(1,dp[i+1][col-1]-dungeon[i][col-1]);
        }
        
        for(int i=row-2;i>=0;i--){
            for(int j=col-2;j>=0;j--){
                dp[i][j]=Math.max(1,Math.min(dp[i+1][j],dp[i][j+1])-dungeon[i][j]);
            }
        }
        return dp[0][0];
    }
}

最长公共子串

子序列：x=(A,B,C,D,E)中z=（A,B,D,E）是X的子序列公共子序列：z是序列x的子序列，同时也是y的自序列

优化子结构：

设X=(x_1,x_2,...,x_m)与Y=(y_1,y_2,...,y_n)是两个序列，Z=(z_1,z_2...,z_k)是X与Y的LCS，则：

如果x_m=y_n,则z_k=x_m=y_n，Z_{k-1}是X_{m-1}和Y_{n-1}的LCS:

$\\LCS(XY)=LCS(X_{m-1}Y_{n-1})+\left \{x_m=y_n \right \}$

如果x_m != y_n,则z_k != x_m,Z_k是X_m-1和Y_{n}的LCS，

$\\LCS(XY)=LCS(X_{m-1}Y_{n})$

如果x_m != y_n,则z_k != y_n,Z_k是X_m和Y_{n-1}的LCS，

$\\LCS(XY)=LCS(X_{m}Y_{n-1})$

 private static int[][] LCSequence(String str1,String str2){
     int[][] matrix=new int[str1.length()+1][str2.length()+1];
     for(int i=0;i<str1.length()+1;i++){
         matrix[i][0]=0;
     }
     for(int j=0;j<str2.length()+1;j++){
         matrix[0][j]=0;
     }
     for(int i=1;i<=str1.length();i++){
         for(int j=1;j<=str2.length();j++){
             if(str1.charAt(i-1)==str2.charAt(j-1))
                 matrix[i][j]=matrix[i-1][j-1]+1;
             else
                 matrix[i][j]=(matrix[i-1][j]>matrix[i][j-1])?matrix[i-1][j]:matrix[i][j-1];
         }
     }
     return matrix;
 }
 
 public static void print(int[][] opt, String X, String Y, int i, int j) { 
     if (i == 0 || j == 0) { 
         return; 
     } 
     if (X.charAt(i - 1) == Y.charAt(j - 1)) { 
         print(opt, X, Y, i - 1, j - 1); 
         System.out.print(X.charAt(i - 1)); 
     } else if (opt[i - 1][j] >= opt[i][j]) { 
         print(opt, X, Y, i - 1, j); 
     } else { 
         print(opt, X, Y, i, j - 1); 
     }
 }

算法复杂度：

$\\O(mn)$

空间复杂度：

$\\O(mn)$

凸多边形的三角剖分

将凸多边形分割成互不相交的三角形的弦的集合T。给定凸多边形P，以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分，使得该三角剖分中诸三角形上权之和为最小。三角剖分如下图所示：

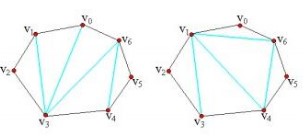
递推公式

$\\t=[i][j] = \left\{\begin{matrix} 0,i=j\\ \underset{i \leq k < j}{min} \left \{ t[i][j]+t[k+1][j]+w(v_{i-1}v_{k}v_{j}\right \},i \leqslant j \end{matrix}\right.$

public class Triangulation {
    private static int N=5;
    private static int[][] weight = {
        {0,2,2,3,1,4},{2,0,1,5,2,3},{2,1,0,2,1,4},{3,5,2,0,6,2},{1,2,1,6,0,1},{4,3,4,2,1,0}
    };
    public static void main(String[] args){
        int [][]s = new int [6][6]; 
        int [][]t = new int [6][6]; 
        System.out.println("此多边形的最优三角剖分值为："+MinWeightTriangulation(N,t,s)); 
        System.out.println("最优三角剖分结构为："); 
        Traceback(1,5,s); //s[i][j]记录了Vi-1和Vj构成三角形的第3个顶点的位置
    }
 
    private static int MinWeightTriangulation(int n,int[][] t,int[][] s){
        for(int i=1;i<=n;i++){
            t[i][i]=0;
        }
        for(int r=2;r<=n;r++){
            for(int i=1;i<=n-r+1;i++){
                int j=i+r-1;
                t[i][j]=t[i+1][j]+Weight(i-1,i,j);
                s[i][j]=i;
                for(int k=i+1;k<j;k++){
                     int u=t[i][k]+t[k+1][j]+Weight(i-1,k,j);
                     if(u<t[i][j]){
                         t[i][j]=u;
                         s[i][j]=k;
                     }
                }
             }
        }
        return t[1][N];
    }
 
    private static void Traceback(int i,int j,int s[][]){
        if(i==j) return;
        Traceback(i,s[i][j],s);
        Traceback(s[i][j]+1,j,s);
        System.out.println("三角剖分顶点：V"+(i-1)+",V"+j+",V"+s[i][j]);
    }
    private static int Weight(int a,int b,int c) 
    { 
        return weight[a][b] + weight[b][c] + weight[a][c]; 
    } 
}

0-1背包问题

给定n种物品和一个背包，物品i的重量是wi，价值vi, 背包容量为C, 问如何选择装入背包的物品，使装入背包中的物品的总价值最大？对于每种物品只能选择完全装入或不装入，一个物品至多装入一次。数学语言描述为：输入：C>0, $w_i$>0, $v_i$>0, 1≤ i≤n 输出：(x1, x2, …, xn), $x_i$∈{0, 1}, 满足$\sum\limits_{ 1 \le i \le n}w_i*x_i \le C$ 例子：有编号为a、b、c、d、e的5件物品，他们的重量分别是2、2、6、5、4，他们的价值分别是6、3、5、4、6，现在给你一个承重为10的背包，如何让背包里装的物品拥有最大的价值？ a8单元格：物品包括a、b、c、d、e，容量为8时，F[i-1,j]=F[b,8]=9，F[i-1,j-Wi]+Pi=F[b,6]+6=9+6=15，两种情况取最大值，因此这里的最大值是15。

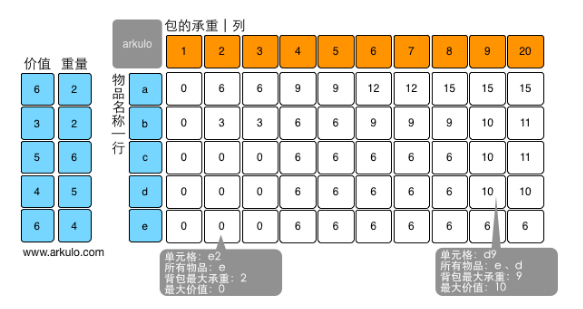
递归方程：

$\\V_{i,j}=Max \left \{ V_{i-1,j-W_i} + P_i , V_{i-1,j} \right \}$

V_{i,j}表示在前i件物品中选择若干件放在承重为j的背包中，可以取得的最大价值。
P_i表示第i件物品的价值。

private static int Package01(int[] W,int[] P,int C){
     int itemNum=W.length;
     int[][] Table=new int[itemNum+1][C+1];
     for(int i=1;i<=itemNum;i++){
         for(int j=1;j<=C;j++){
             Table[i][j]=Table[i-1][j];
             if(j>=W[i-1]&&Table[i-1][j-W[i-1]]+P[i-1]>Table[i][j]){
                 Table[i][j] = Table[i-1][j-W[i-1]]+P[i-1];
             }
         }
     }
     return Table[itemNum][C];
 }

算法复杂度：

$\\O(vn)$

空间复杂度：

$\\O(vn)$

Edit Distance

Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.) You have the following 3 operations permitted on a word: a) Insert a character b) Delete a character c) Replace a character

递推公式

$\\D_{m,n} = min \left\{\begin{matrix} D_{m-1,n-1}+c(a_m,b_n)\\ D_{m-1,n}+1\\ D_{m,n-1}+1 \end{matrix}\right.$

class Solution {
    public int minDistance(String word1, String word2) {
        int len1 = word1.length();
        int len2 = word2.length();
        int[][] dp = new int[len1+1][len2+1];
        for(int i=0;i<len2+1;i++){
            dp[0][i]=i;
        }
        for(int i=0;i<len1+1;i++){
            dp[i][0]=i;
        }
        int c=0;
        for(int i=1;i<len1+1;i++){
            for(int j=1;j<len2+1;j++){
                if(word1.charAt(i-1)==word2.charAt(j-1))
                    c=0;
                else c=1;
                dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+c);
            }
        }
        return dp[len1][len2];
        
    }
    private static int min(int a,int b,int c){
     int result=a<b?(a<c?a:c):(b<c?b:c);
     return result;
    }
}

合唱团

题目描述有 n 个学生站成一排，每个学生有一个能力值，牛牛想从这 n 个学生中按照顺序选取 k 名学生，要求相邻两个学生的位置编号的差不超过 d，使得这 k 个学生的能力值的乘积最大，你能返回最大的乘积吗？输入描述:
每个输入包含 1 个测试用例。每个测试数据的第一行包含一个整数 n (1 <= n <= 50)，表示学生的个数，接下来的一行，包含 n 个整数，按顺序表示每个学生的能力值 ai（-50 <= ai <= 50）。接下来的一行包含两个整数，k 和 d (1 <= k <= 10, 1 <= d <= 50)。
输出描述:
输出一行表示最大的乘积
示例1 输入
3
7 4 7
2 50
输出
49

递推公式

$\\dpMax_{i,j} = max \left \{ dpMax_{i-x,j-1}*array_i, dpMin_{i-x,j-1}*array_i\right \}$

$\\dpMin_{i,j} = min \left \{ dpMax_{i-x,j-1}*array_i, dpMin_{i-x,j-1}*array_i\right \}$

$\\dp = \left[ {\begin{array}{*{20}{c}} {a_0}&{a_0}&{0}&{\cdots}&{0}&{0}\\ {a_0}&{a_0}&{a_0*a_1}&{\cdots}&{0}&{0}\\ {\vdots}&{\vdots}&{\vdots}&{\vdots}&{\vdots}&{\vdots}\\ {a_0}&{a_{n-2}}&{\cdots}&{?}&{?}&{?}\\ {a_0}&{a_{n-1}}&{\cdots}&{?}&{?}&{a_{n-1}*\cdots} \end{array}} \right]$

第i行第j列表示以a_i结尾的长度为j的序列的最大/最小的乘积

import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        while (in.hasNext()) {
            int n = in.nextInt();
            int[] power = new int[n];
            for (int i = 0; i < n; i++) {
                power[i] = in.nextInt();
            }
            int k = in.nextInt();
            int d = in.nextInt();
            System.out.println(MaxPower(power, k, d));
        }
    }
    private static long MaxPower(int[] power, int k, int d) {
        // TODO Auto-generated method stub
        long dpMax[][] = new long[power.length][k + 1];
        long dpMin[][] = new long[power.length][k + 1];
        for (int i = 0; i < power.length; i++) {
            dpMax[i][1] = power[i];
            dpMax[i][0] = power[0];
            dpMin[i][1] = power[i];
            dpMin[i][0] = power[0];
        }
        long res = Long.MIN_VALUE;
        for (int j = 2; j <= k; j++) {
            for (int i = j - 1; i < power.length; i++) {
                dpMax[i][j] = Long.MIN_VALUE;
                dpMin[i][j] = Long.MAX_VALUE;
                for (int x = 1; x < d && (i - x) >= j - 2; x++) {
                    long resMax = Math.max(dpMax[i - x][j - 1] * power[i],
                            dpMin[i - x][j - 1] * power[i]);
                    long resMin = Math.min(dpMax[i - x][j - 1] * power[i],
                            dpMin[i - x][j - 1] * power[i]);
                    if (resMax > dpMax[i][j]) {
                        dpMax[i][j] = resMax;
                    }
                    if (resMin < dpMin[i][j]) {
                        dpMin[i][j] = resMin;
                    }
                }
            }
        }
        for (int i = k - 1; i < power.length; i++) {
            if (dpMax[i][k] > res) {
                res = dpMax[i][k];
            }
        }
        return res;
    }
}

Unique Paths

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below). The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below). How many possible unique paths are there? Above is a 3 x 7 grid. How many possible unique paths are there? Note: m and n will be at most 100.

方法一：动态规划

class Solution{
    public int uniquePaths(int m,int n){
        int[][] dp= new int[m][n];
        dp[0][0]=1;
        for(int i=1;i<m;i++){
            dp[i][0]=1;
        }
        for(int i=1;i<n;i++){
            dp[0][i]=1;
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

方法二：数学法

class Solution {
    public int uniquePaths(int m, int n) {
        if(m==1||n==1) return 1;
        int step = m-1+n-1;
        long res = 1;
        int temp = Math.min(m,n);
        for(int i=step;i>=(step-(temp-1)+1);i--){
            res*=i;
            res/=(step+1-i);
        }
        return (int)res;
    }
}

Follow up for “Unique Paths”: Now consider if some obstacles are added to the grids. How many unique paths would there be? An obstacle and empty space is marked as 1 and 0 respectively in the grid. For example, There is one obstacle in the middle of a 3x3 grid as illustrated below.
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
The total number of unique paths is 2.

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp= new int[m][n];
        for(int i=0;i<m;i++){
            if(obstacleGrid[i][0]!=1)
                dp[i][0]=1;
            else
                break;
        }
        for(int i=0;i<n;i++){
            if(obstacleGrid[0][i]!=1)
                dp[0][i]=1;
            else
                break;
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(obstacleGrid[i][j]!=1)
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

Interleaving String

Given s1, s2, s3, find whether s3 is formed by the interleaving of s1 and s2. For example, Given: s1 = “aabcc”, s2 = “dbbca”, When s3 = “aadbbcbcac”, return true. When s3 = “aadbbbaccc”, return false.

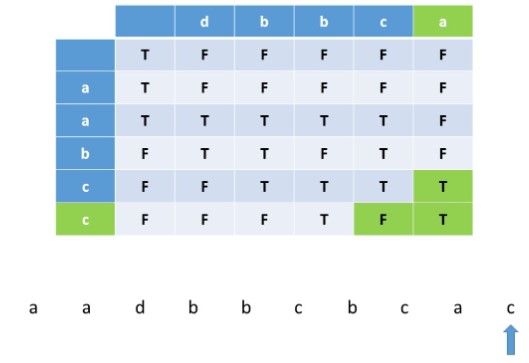
class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        int len1 = s1.length();
        int len2 = s2.length();
        int len3 = s3.length();
        if(len1+len2!=len3) return false;
        int[][] dp = new int[len1+1][len2+1];
        dp[0][0]=1;
        for(int i=1;i<len2+1;i++){
            if(s2.charAt(i-1)==s3.charAt(i-1)&&dp[0][i-1]==1)
                dp[0][i]=1;
        }
        for(int i=1;i<len1+1;i++){
            if(s1.charAt(i-1)==s3.charAt(i-1)&&dp[i-1][0]==1)
                dp[i][0]=1;
        }
        for(int i=1;i<len1+1;i++){
            for(int j=1;j<len2+1;j++){
                if(s2.charAt(j-1)==s3.charAt(i+j-1)&&dp[i][j-1]==1)
                    dp[i][j]=1;
                if(s1.charAt(i-1)==s3.charAt(i+j-1)&&dp[i-1][j]==1)
                    dp[i][j]=1;
            }
        }
        return dp[len1][len2]==1;
    }
}

最优打包

一个淘宝的订单中包含n(10>=n>=1)种商品A1，A2，…，An，每种商品数量分别为a1，a2，…，an个，记做{a1,a2,…,an}(ak>0)。订单在仓库生产过程中，仓库为了提升作业效率，会提前对热门组合商品进行预包装。假设这n个商品有m(9>=m>=1)个商品组合，每个组合bomk包含A1，A2，…，An的数量分别为{b1,b2,…,bn}(bk>=0,至少存在一个bk>0) 举例如下： 订单包含A，B，C商品，数量为{2，3，1}，商品组合bom1{2，1，1}，bom2{1，1，0}，bom3{0，1，1} 对以上订单匹配给定商品组合，得到的可能匹配结果为：res1.匹配到组合1一套，剩余B商品；res2.匹配到组合2两套，组合3一套，不剩商品；现要求订单的最优匹配，最优匹配的原则为：

匹配组合后，剩余商品种类数越少越好；

在剩余商品种类数相同的情况下，匹配到的组合种类数越少越好；

例如上面例子，我们认为res2优于res1。现需要编写程序，输入格式为： n,m a1,a2,…,an bom1,b11,b12,…,b1n bom2,b21,b22,…,b2n …. bomm,bm1,bm2,…,bmn 输入数据的格式说明（数据间使用英文逗号分隔）：第一行数据：n个商品，m个预包方案第二行数据：商品1个数，商品2个数，。。。，商品n个数第三行数据：bom1，商品1个数，商品2个数，。。。，商品n个数第n-1行数据：。。。。第n行数据：bomn，商品1个数，商品2个数，。。。，商品n个数针对输入数据找出最优匹配，输出最优匹配的组合及套数，比如针对上面的例子输出： match result: bom22，bom31

动态规划

动态规划（dynamic programming）

Longest Increasing Subsequence

Climbing Stairs

House Robber

Maximum Subarray

Coin Change

Triangle

Minimum Path Sum

Dungeon Game

最长公共子串

凸多边形的三角剖分

0-1背包问题

Edit Distance

合唱团

Unique Paths

Interleaving String

最优打包

CATALOG

FEATURED TAGS

FRIENDS